Rで数独を解いてみた。その中で、R独特の機能が結構有効であったので、解説してみる。サンプルとして、Take-Shobo「ナンプレ超極・激」の30番を使用した。次のような問題である。
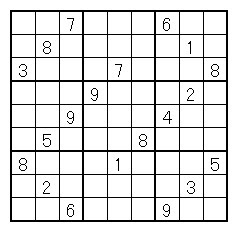
結果は
整形してないので見にくいが、9文字ごとに改行を入れると答えになる。もちろん先頭の[1]などは除いて。
Rのプログラムというのだろうか、ソースは以下のようなものである。
1行目、qが問題である。81文字の数字で、0は空欄を表す。q すなわち question である。
2行目、qを1文字ずつに分解し、更に数値に変換している。0~9の数字81個のベクトルである。名前bはボードの意である。
プログラムの中で、bは重要な位置を占める。
数独の問題は、視覚的には平面であるが、プログラム内では1次元ベクトルとして表現している。実は、この方がよいのである。そのことはだんだんと分かってくる。
数独のマスに順に1~81までの番号を付け、この番号を「座標」と呼ぶことにする。座標はiであらわす。
3行目から10行めはグループの指定である。
数独では各1行の中に1~9のすべての数字が入る。各1列の中にも同様である。さらに、3×3に分けた9個の各正方形の中においても同様である。この、行・列・3×3正方形の1つずつを「グループ」と呼ぶことにする。gsは各グループの座標を持つ行列である。gsはグループスの意味である。内容は次のようになる。
[1,]は1行目を表す。[10,]は1列目を表す。[19,]は左上の3×3正方形を表す。
gsを用いて、各グループに同じ数字がないことを確認するのである。実は思いがけない利用法がある、対角線上に1~9があることを条件としたり、変な形の領域に1~9があることを条件にする問題があるが、ここを変えればよいのである。
グループは27個あり、その番号はkで指定する。また、一つのグループはベクトルgで表す。
11行めから44行めの関数checkが肝である。
引数が複雑だが、外から使うときはcheck(b)のように使えばよい。このように使うと、12行めで行列sbを作る。
このsbがこのプログラムのもう一つの重要点である。サブボードのつもりでsbという名前を付けた。
ボードの各マスには1~9のいずれかの数字が入るのだが、その候補を記録するのがsbである。
sbは81行9列の行列で、各行が、各座標に入る数字の候補を記録している。
sb[i,n]は、座標iに数字nが入る可能性があれば1、なければ0をとる。
例えば1行目が 1,1,0,0,0,0,1,1,1 となっているとすると、座標1のところには、1,2,7,8,9のいずれかが入る。逆に言えば3,4,5,6は入らないことを意味する。
sbの候補をどんどん減らしていって答えを見つけるのである。
最初はすべて1である。すなわち、すべての数字の入る可能性がある。
どのように候補を絞っていくかが、そのあとに続く。
15・16行めは、ボードに数字が入っている場合、すなわち0でない場合は、その座標のsbは、その数字のところを1とし、それ以外を0とする。
b[i]は座標iの位置にある数字である。「sb[i,-b[i]]=0」はsbのi行めのうちの、「b[i]すなわち座標iの数字」以外のところを0にする。普通の言語だとループでやるところだ。こんなに簡単にできる。(簡単というのは表現の文字数が少ないという意味だ。表現の理解はそう簡単ではない)
18行めから26行め。for文を使ってしまった。applyか何かでやりたいところだが、今後の課題。
ここでは、ボード上で数字が入っていたら、その座標を含むグループのほかの座標ではその数字は使えないので、sbのその位置を0にする。もっと具体的に言うと、座標iの位置にある数字がnのとき、座標iを含むグループの他の座標jについて、sb[j,n]を0にするのだ。
プログラムに沿って解説する。
kはグループ番号で、1~27まで変わる。
k番目のグループをgとする。gは長さ9のベクトルで、k番目のグループの座標を持っている。
pはg内をポイントし、1~9変わる。
g[p]がグループgのp番目の座標なので、その位置の数字はn=b[g[p]]となる。nが0の時は数字はないので何もしない。0でないときは座標g[p]に数字nがあるので、そのグループ内のほかの座標のsbのnのところを0にしなければならない。なんとそれが、
sb[g[-p],n]=0でできてしまう。g[-p]はグループgのポイントしている以外のすべての座標からなるベクトルだ。それらの行のn番目を0にするのだ。
ここまではbの情報をもとにsbを変更した。
次の27行めから30行めは、sbをもとに、bを変更する部分である。
iはボード上の座標である。1~81の値をとる。
sb[i,]は座標iのサブボード情報である。すなわち、各数字が可能性があるかどうかを示す9つの数(0か1)からなる。
sum(sb[i,])が0だということは、その座標に入る数字がないことになる。すなわち、解(甲斐)なしである。NULLを返すこととした。
sum(sb[i,])が1だということは、座標iに入る数字が一つに決まったということである。その場合はボードに数字を書き込む。
15行めから30行目までを繰り返すと、易しい問題は解ける。繰り返しは必要で、sbからbに変更が加わるとそのbからまたsbに変更が生し、・・・ということがあるからである。13行めから42行目までがrepeatで囲まれているのはそのためである。
繰り返して、変更がなくなったらrepeatを抜けるのだが、その判断は、sbのフラグの総数の変化で調べている。sbのフラグ(1)の総数は単調減少だ。
31行めから40行めの説明は後回しにする。
43行め、返す値は、ボードbとサブボードsbのリストである。
checkだけで解ける問題は易しい問題である。checkだけでは解けない問題を試行錯誤で解くようにしたのがsolveである。
solveは最初の空欄に1~9までの数字を当てはめてcheckを繰り返す。1段階の当てはめでうまくいかない場合は、再帰的に多段階で挑戦させる。
solveの引数はl(エル)である。checkで返すリストを引数にする。リストなのでlだ。l[[1]]はボード、l[[2]]はサブボードだ。サブボードは渡さなくても計算できるが、せっかくそれまで計算したものをはじめから計算するのもどうかと思って、引数として渡すことにした。
さて、最後に残った31行めから40行めだ。
当初、これはつけないつもりでいた。試行錯誤させればよいと考えていたからだ。ところがサンプルの問題では1時間ほど動かしても答えが出ない。空欄が多い問題ではこうなるのは必然だ。
ここでやっていることは、1つのグループ内のsbのフラグをすべて見て、例えば5のフラグが1個しか立っていないならば、そこが5だ
ということを調べている。
このルーチンを付け加えたら、サンプル問題は一瞬で解けた。試行錯誤なしで、checkのみで解けた。「超極・激」というには情けない。まあ、30番だから。このあと難しいのがあるのだと思う。
このように実際の数独を解くときに使う戦略を組み込むと速度は劇的に改善する。今回Rで作ってみたが、以前に一度python3でプログラムしたことがある。その時の経験に基づいた発言である。
以上でこの稿は終わる。
しばらく、更新してなかったので、更新しなければという強迫観念で書いた。
きっと読みにくいだろうと思う。
面白いと思ってくれる人がいるのだろうか?